Enhedscirklen
Enhedscirklen er en cirkel med radius = 1.
Cosinus, sinus og tangens
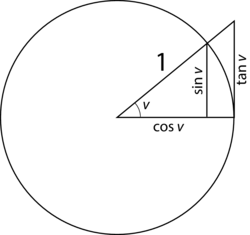
De trigonometriske udtryk sinus, cosinus og tangens defineres v.h.a. enhedscirklen.
Tangens bestemmes også som:
$${\tan v = \frac{\sin v}{\cos v} }$$
I enhedscirklen gælder desuden Grundrelationen:
$${ \sin^2{(v)} + \cos^2{(v)} = 1 }$$
Den retvinklede trekant
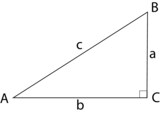
I den retvinklede trekant ABC gælder:
$${ \sin A = \frac{a}{c},\quad \cos A = \frac{b}{c},\quad \tan A = \frac{a}{b} }$$
$${ \sin B = \frac{b}{c},\quad \cos B = \frac{a}{c},\quad \tan B = \frac{b}{a} }$$
I den retvinklede trekant gælder desuden Pythagoras' læresætning:
$${ a^2 + b^2 = c^2 }$$
Den vilkårlige trekant
I den vilkårlige trekant ABC gælder cosinus- og sinusrelationerne:
Sinusrelationen:
$${ \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c} }$$
Cosinusrelationen:
$${ a^2 = b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos A }$$
Cirklen
En cirkels areal:
$${ T = \pi \cdot r^2 }$$
En cirkels omkreds:
$${ O = 2 \cdot \pi \cdot r }$$
Vinkler i cirklen
En centervinkel har toppunkt i cirklens centrum.
En periferivinkel har toppunkt på cirkelperiferien.
Hvis en periferivinkel og en centervinkel spænder over den samme cirkelbue, vil det gælde, at centervinklen er dobbelt så stor som periferivinklen.
Tangent
En tangentlinje tangerer cirklens periferi i ét punkt, tangentpunktet.
Korde
Et linjestykke, der forbinder to punkter på cirkelperiferien, kaldes en korde.
Kordens længde \(K\) bestemmes vha. den vinkelbue som korden spænder over:
$${ K = 2 \cdot r \cdot \sin{\left( \frac{v}{2} \right)} }$$
Pilhøjde
En pilhøjde \(h\) er et linjestykke der går fra et punkt \(P\) på cirkelperiferien, og som står vinkelret på midten af korden. \(h\) bestemmes vha. formlen:
$${ h = r \cdot \left( 1 - \cos{\left( \frac{v}{2} \right)}\right) }$$
Cirkeludsnit
Arealet af et cirkeludsnit er givet ved:
$${ T = \pi \cdot r^2 \cdot \frac{v}{360^\circ} }$$
hvor \(v\) er vinklen som cirkeludsnittet er bestemt af.
Længden af en cirkelbue, der spænder over en vinkel, \(v\):
$${ l = 2 \cdot \pi \cdot r \cdot \frac{v}{360^\circ} }$$
Cirkelafsnit
Arealet af et cirkelafsnit, hvor vinklen v måles i grader:
$${ T = r^2 \left(\frac{\pi \cdot v}{360^\circ} - \frac{\sin v}{2} \right) }$$
Arealet af et cirkelafsnit, hvor vinklen v måles i radianer:
$${ T = r^2 \cdot \left( \frac{v}{2} - \frac{\sin v}{2} \right) }$$
hvor:
$${ 1\ radian = \frac{360^\circ}{2\pi} \approx 57,296^\circ }$$
Trekantens indskrevne cirkel
Arealet af en vilkårlig trekant givet ved den indskrevne cirkel:
$${ T = \frac{1}{2} r \cdot (a + b + c) }$$
Trekantens omskrevne cirkel
Arealet af en vilkårlig trekant givet ved den omskrevne cirkel:
$${ T = \frac{a \cdot b \cdot c}{4 \cdot r} }$$

