Integrationsmetoder

Sum og differens af funktioner: $${ \int f(x) \pm g(x) dx = \int f(x) dx \pm \int g(x) dx }$$

Multiplikation med konstant: $${ \int kf(x) dx = k \int f(x) dx }$$

Integration ved substitution: $${ \int f(g(x)) g'(x) dx = F(g(x)) = \int f(t) dt \text{, hvor } t = g(x) }$$

Bestemt integration ved substitution: $${ \int_{a}^{b}f(g(x)) g'(x) dx = \int_{g(a)}^{g(b)}f(t) dt }$$

Partiel integration: $${ \int f(x) g(x) dx = F(x) g(x) - \int F(x)g'(x)dx }$$

Rumfang af grafer til kontinuerte funktioner roteret om x-aksen

Når en kontinuert positiv funktion $f$ deﬁneret i intervallet $x_1 < x < x_2$ drejes $360^o$ om x-aksen, opstår et rumligt objekt med rumfanget $${ V_x = \int_{x_1}^{x_2} \pi \left( f(x) \right)^2 dx }$$

Rumfang af arealet imellem to grafer roteret om x-aksen

For to positive kontinuerte funktioner deﬁneret i intervallet $x_1 < x < x_2$ opstår der et rumligt objekt, når arealet imellem de funktioners grafer og linjerne $x = x_1$ og $x = x_2$ roteres $360^o$ om x-aksen. Rumfanget bestemmes som $${ V_x = \pi \int_{x_1}^{x_2} (g(x))^2 - (f(x))^2 dx }$$

Rumfang af grafer til kontinuerte funktioner roteret om y-aksen

Når en kontinuert positiv funktion $f$ defineret i intervallet $x_1 < x < x_2$ drejes $360^o$ om y-aksen, opstår et rumligt objekt med rumfanget $${ V_y = 2 \pi \int_{x_1}^{x_2} f(x) \cdot x dx }$$

Rumfang af arealet imellem to grafer roteret om y-aksen

For to positive kontinuerte funktioner defineret i intervallet $x_1 < x < x_2$ opstår der et rumligt objekt, når arealet imellem de funktioners grafer og linjerne $x = x_1$ og $x = x_2$ roteres $360^o$ om y-aksen. Rumfanget bestemmes således $${ V_y = 2 \pi \int_{x_1}^{x_2} (g(x) - f(x) ) \cdot x dx }$$

Kurvelængder

For en differentiabel funktion i intervallet $ [x_1, x_2] $ findes kurvelængden ved følgende integral: $${ l_f = \int_{x_1}^{x_2} \sqrt{1 + f'(x)^2 } dx }$$

Overfladeareal af rumlig figur dannet ved rotation af graf om x-aksen

For en kontinuert funktion $f$ deﬁneret i intervallet $ [x_1, x_2] $ findes overfladearealet af det legeme, der opstår, når området imellem grafen for f og x-aksen roteres $360^o$ om x-aksen: $${ O = 2 \pi \int_{x_1}^{x_2} f(x) \sqrt{1 + f'(x)^2} dx }$$

Massemidtpunktet for arealet imellem to kurver

For to kontinuerte funktioner $f$ og $g$, hvor $f > g$ i intervallet $ [a, b] $, ﬁndes massemidtpunktet som $${ \begin{aligned} (x_m, y_m) &= \left( \frac{M_y}{A}, \frac{M_x}{A} \right) \\ &= \left( \frac{ \int_a^b \left( f(x) - g(x) \right) \cdot x dx} {\int_a^b \left( f(x) - g(x) \right) dx}, \frac{\int_a^b \frac{1}{2} \left( f(x)^2 - g(x)^2 \right) dx } {\int_a^b \left( f(x) - g(x)\right) dx} \right) \end{aligned} }$$

Tyngdepunkter for kendte geometriske grundfigurer

Cirkelafsnit

Tyngdepunkt for et cirkelafsnit findes som $${ r_t = \frac{k^3}{12 \cdot A} }$$ $k$ er kordelængde, $A$ areal, og $r_t$ er afstanden fra tyngdepunkt til cirklens centrum.

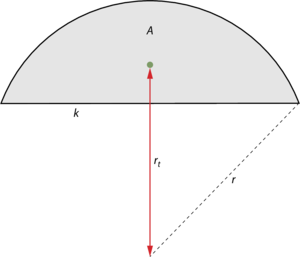
Cirkelafsnit

Cirkeludsnit

Tyngdepunkt for et cirkeludsnit findes som $${ r_t = \frac{2 \cdot k \cdot r}{3 \cdot b} }$$ $k$ er kordelængde, $b$ er længden af buestykket, $r$ er radius, og $r_t$ er afstanden fra tyngdepunkt til cirklens centrum.

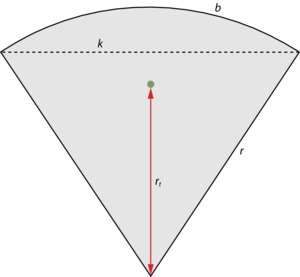
Cirkeludsnit