Længden af et linjestykke
Længden af et linjestykke som diagonal i en retvinklet kasse med sidelængderne l, b, h
$${ d = \sqrt{l^2 + b^2 + h^2}}$$
Afstandsformlen
Afstanden \(d\) mellem to punkter \(A = (Ax, Ay, Az)\) og \(B = (Bx, By, Bz)\)
$${ d = \sqrt{(A_x - B_x)^2 + (A_y - B_y)^2 + (A_z - B_z)^2} }$$
Stedvektor
Punkt \(A = (Ax, Ay, Az)\) vektor
$${ \vec{0A} = \begin{pmatrix} A_x \\ A_y \\ A_z \end{pmatrix} }$$
Punkt \(B = (Bx, By, Bz)\) vektor
$${ \vec{0B} = \begin{pmatrix} B_x \\ B_y \\ B_z \end{pmatrix} }$$
Vektor
$${ \vec{AB} = \vec{0B} - \vec{0A} }$$
Vektorlængde
$${ |\vec{AB}| = \sqrt{(A_x - B_x)^2 + (A_y - B_y)^2 + (A_z - B_z)^2} }$$
Ret prisme
Rumfang
$${ V = G \cdot h }$$
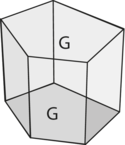
Et ret femkantet prisme
Cylinder
Rumfang
$${ V = \pi \cdot r^2 \cdot h }$$
Krum overflade
$${ T = 2 \cdot \pi \cdot r \cdot h }$$
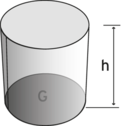
Cylinder
Kugle
Rumfang
$${ V = \frac 4 3 \cdot \pi \cdot r^3 }$$
Areal af overflade
$${ T = 4 \cdot \pi \cdot r^2 }$$
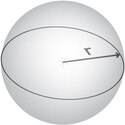
Kugle med radius \(r\)
Kugleafsnit
Rumfang
$${ V = \pi \cdot h^2 \cdot \left( r - \frac{h}{3} \right) }$$
Areal af krum overflade
$${ T = 2 \cdot \pi \cdot r \cdot h}$$
eller
$${ T = \pi \cdot (a^2 + h^2) }$$
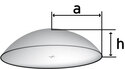
Kugleafsnit
Pyramide
Rumfang
$${ V=\frac{1}{3}\cdot h\cdot G }$$
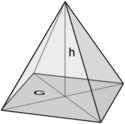
Pyramide
Pyramidestub
Rumfang
$${ V = \frac{1}{3}\cdot h \cdot (G + g + \sqrt{G \cdot g}) }$$
Areal af én sideflade
$${ T = \left( \frac{a+b}{2} \right) \cdot \sqrt{h^2 + s^2} }$$
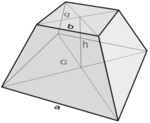
Pyramidestub
Kegle
Rumfang
$${ V = \frac{\pi}{3} \cdot h \cdot r^2 }$$
Areal af krum overflade
$${ T = \pi \cdot r \cdot s}$$
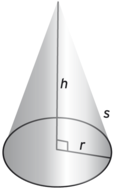
Kegle
Keglestub
Rumfang
$${ V = \frac{\pi}{3} \cdot h \cdot (R^2 + r^2 + R \cdot r) }$$
Areal af krum overflade
$${ T = \pi \cdot s \cdot (R+r) }$$
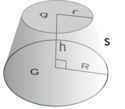
Keglestub
Guldins regler
Overfladeareal
Guldins 1. regel
$${ T = \pi \cdot a \cdot l \cdot \frac{v}{180^\circ} }$$
Rumfang
Guldins 2. regel
$${ V=a\cdot T_f\cdot 2\cdot \pi\frac{v}{360^o} }$$
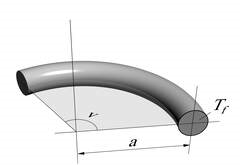
Omdrejningslegeme








